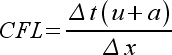Solution
Options
Once the problem is completely set up, the next
step is to solve the problem. Solution is generated using the Solution
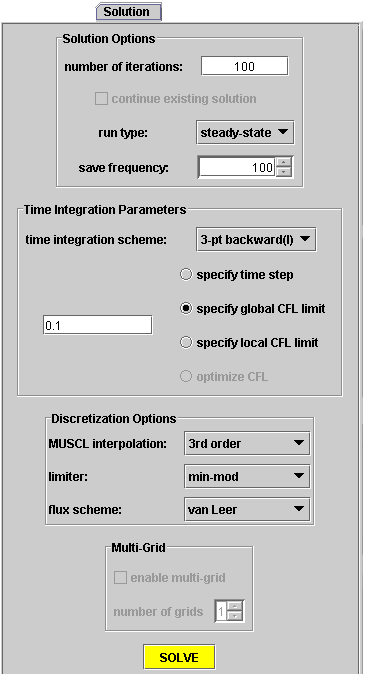
navigation tab. This tab is shown in Fig. 17.
Figure 17. Detailed
View of the Solution Navigation Tab
Solution is straightforward, but there are several
major options which must be considered before proceeding. These options
are sorted into broad categories a shown above in Fig. 17.
First are basic solution options. The number
of iterations specifies how many new solution iterations to perform during
the next run. Since the Euler equations are non-linear, they cannot
be solved directly. Even for steady state problems, suitable initial
conditions must be chosen, and the solution iterated until sufficient convergence
is achieved. This issue will be discussed more under evaluating the
solution. The number of iterations required varies and is difficult
to predict. Simple problems may converge in only a few hundred iterations
while more complex nozzle configurations may require several thousand.
Time accurate problems will obviously be dependent on the time window
that the user is interested in, and the resolution within that tiem window
to create an accurate history. The check box below the iterations
specifies whether to continue the existing solution or start fresh from
the specified initial conditions. If there is no solution present,
this is grayed out and Gryphon automatically initializes the grid from the
initial conditions specified in the previous section. If there is
a choice, the user has the option of continuing fro mthe most recent solution
point to further converge the solution or start over (if the box is not
checked). Next, the run type can be selected to be either steady-state
or transient to describe the type of analysis to be performed.
If there is already a solution present and the user
changes the run type, what happens depends on the selections made. If
the existing solution is a steady solution, and the user switches to transient
for a new run, Gryphon quietly sets up the solution to make the exisiting
steady solution the initial conditions at a time of 0.0 and starts the
transient run from there. If the existing solution is transient and
the user switches to steady-state, Gryphon warns the user that doing this
will result in all the time dependent data being destroyed except the most
recent time level. This level becomes the starting solution for the
steady run. The save frequency button does nothing for a steady analysis
and only has an effect on a transient analysis. This item tells Gryphon
how often to save the time level permanently. During a transient run,
Gryphon automatically saves the initial time step, and then saves every
multiple of the save frequency, plus the very last time step of the run if
it doesn't happen to fall on a save frequency. Thus, for example,
running 125 iterations with a save frequency of 50 stores 4 time level solutions
at 0, 50, 100, and 125 iterations.
The time integration box tells Gryphon how to do the
time integration for either a steady or transient problem. First, the
scheme should be picked. There are three implicit schemes and three
explicit schemes to choose from. They are detailed as follows:
- Euler Explicit - this explicit scheme is the most basic
one. It offers the lowest level of time accuracy, but is the fastest
executing scheme. Especially for steady problems where time accuracy
is unimportant, Euler explicit is a good choice.
- Euler Implicit - this implicit scheme is an implicit version
of the Euler explicit. It also offers a relatively low level of time
accuracy. The advantage of implicit schemes is that they allow much
larger time steps to be taken than explicit schemes. In higher dimensions,
this offers a great advantage. In 1-D however, the enhancement is
not as impressive. Further, the necessity of calculating the flux
Jacobian and then solving a pentadiagonal equation system slows down the
solution speed by a factor of several times. This makes the advantage
of using an implicit method somewhat dubious for this case.
- Trapezoidal - The trapezoidal scheme is an implicit scheme
offering more time accuracy than the Euler Implicit scheme. It has
roughly the same speed as the Euler Implicit scheme and thus is a reaonable
choice if one wishes to use implicit schemes.
- 3 Point Backwards - The three point backwards scheme is
a three level implicit scheme utilizing two previous time levels of solution.
This scheme also has higher time accuracy, but the extra cost of
tracking and including an extra time level of information makes this scheme
somewhat slow compared even to the other implicit schemes. Thus, it
is probably not often worth the extra cost.
- Leap frog - The leap frog scheme is an explicit scheme utilizing
two past time levels of solution to generate a higher order of time accuracy
than Euler explicit. However, the leap frog method is known to be
mildly instable, and so difficult to get started properly. It is not
generally recommended over Euler explicit.
- m-Stage Runge Kutta - The Runge Kutta method is an explicit
method which offers good time accuracy. It is the only method that
is not a two parameter time scheme. The Runge Kutta method is a popular
method in CFD. It is a fast execution scheme. In the case of
Gryphon, some extra overhead is required in the scheme to make it compatible
with the other schemes -- which slows it down a bit more than it might on
its own.
In general, the two Euler schemes -- implicit and explicit -- are
recommended the most for problems. Euler explicit is recommended
for steady problems. The CFL restriction (below) is more than made
up for by the quickness of the scheme.
With the scheme known, the method for calculating the
time step advancement at each iteration must be chosen. One may elect
to specify an actual time step in dimensional terms, but it is more common
to specify a CFL condition for the problem. The CFL is a free parameter
governing the ratio of modifying constants in the finite volume stenciling.
The CFL is a dimensionless number, which is non-dimensionalized via
the largest eigenvalue of the system. It is defined as given in eqn.
(1).
|
(1)
|
The CFL is the commonly used method of specifying a timestep because convergence
and stability of the solution is governed by this value and not the actual
time step value. For explicit schemes, there is a CFL restiction. This
restiction is predicted to be a maximum CFL of 0.50, but numerical issues
and boundary conditions lower this limit in actual application somwhat. Depending
on the problem in Gryphon, the explicit schemes will becomes unstable and
diverge at a CFL of around 0.45 or so. Likewise, implicit schemes
have no theoretical CFL restiction. Actual application in Gryphon,
however, shows that CFL values above the range of 1.5 to 2.0 or so tend
to be somewhat unstable, especially in the initial stages of solution. As
indicated above, this limit allows implicit schemes to arrive at solution
approximately 4 time faster than explicit schemes, but they tend to be 4-5
times slower to calculate per iteration. Therefore, in Gryphon, the
choice of implicit or explicit schemes is really a matter of style and preference.
With the definition of the CFL as given in eqn. (1),
Gryphon sweeps through all cells and takes the time step based on the most
restictive cell. Since complex problems often have largely staggered
cell sizes, this can mean that a few cells are severely limiting the majority
of cells by setting their effective cell CFL values to very low numbers.
Enhanced convergence properties have been shown to be obtainable by
using s technique called local time stepping. In this technique, each
cell is individually solved for by taking the maximum allowable time step
for that individual cell. Thus, some cells take larger time steps than
others. This technique can only be used for steady problems as time
accuracy becomes completely meaningless for transient problems if this were
to be done. Hence, this radio button is not selectable for transient
problems. The accelerated convergence of some cells helps to converge
the whole flow field and keeps the solution from stagnating based on the
restriction from one or two cells. The enhancement is generally proportional
to the size difference between the various cells of the grid. In problems
with largely staggered grids, local time stepping can make an order of magnitude
increase in convergence rate.
Finally, the optimum CFL step is only active for transient
problems. Currently, this option just applies a global CFL of 1.0 to
the transient problem. It is mostly a placeholder for future development
in creating an adaptive time integration technique in Gryphon.
Next, in the spatial discretization panel, the user
has choices for several options. First, the order of the spatial reconstruction
must be chosen. The default is 3rd order reconstruction. This
is a good choice for most problems unless the problem shows convergence issues.
If so, a lower order reconstruction may be chosen. The user
may pick from various 1st or 2nd order possiblities as an alternate choice.
All reconstruction techniques are based on MUSCL conservative variable
reconstruction.
The limiter choice is intricately tied to the reconstruction
choice. A problem which uses 1st order reconstruction does not need
to use a limiter, so this area becomes non-useable when 1st order reconstruction
is picked. For higher order reconstruction however, sharp changes in
the solution such as those caused by shockwaves can generate non-physical
oscillations in the solution. This can easily be demonstrated to the
user by selecting third order reconstruction and specifically setting no
limiter in the code after setting up a problem which will have a shock in
the solution. Large oscillations will appear. This is caused by
diffusion in the numerical scheme. Geometrically, the high order reconstruction
causes the scheme to show cell face variable values that are "out-of-bounds"
or beyond the range of possibility due to the sharp changes near the face.
A limiter accounts for this by limiting the possible range which a
conservative variable and hence a cell flux can be set to, thus damping out
the oscillations. A limiter is designed to do very little except in
the region near a shock. Only there does it become active and prevent
oscillations. There are several of the most common choices for limiters
programmed into Gryphon. The one thing to note is that the MIN-MOD
limiter can sometimes enter into what is termed "limit cycling." This
effect causes the residual to stop decreasing and oscillate infinitely after
2-3 orders of magnitude decrease. This is caused by the discontinuous
nature of that limiter.
Finally, one of the most important choices to be made
is in the choice of flux prediction. Three techniques for handling
the spatial flux terms are given: Van Leer flux splitting, AUSM flux splitting,
and Roe flux difference splitting. All three are common, contemporary
techniques for solving wave problems. The Roe technique is the technique
that offers the most accuracy and is the preferred technique of many researchers.
However, it is slower, more complex, and less numerically robust than
the other two. The Roe scheme does employ a Harten-like entropy correction
to prevent the presence of expansion shocks in the flow.
Last, at the bottom of the Solution navigation tab
is the "Solve" button, highlighted in yellow. This is an improtant
button in Gryphon, as it starts a solution based on all the input up to
this point. After pressing "solve," the user is presented with a dialog
showing a progress bar of the solution status. The line graph window
will begin to show a residual history that is updated real-time. If
the user wishes to stop the solution before running all of the requested
iterations, the dialg box provides a button to stop the solution early. Pressing
this button will cause Gryphon to finish its iteration and save that data
as the final state before stopping.
If something is wrong in the formulation and Gryphon
detects that the solution has diverged, it will stop solving and display
a dialog box stating so. It is best at that point to reset the solution
and make changes to the solution options or model to take care of the instability.