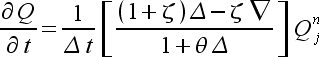
| <previous: Finite Volume Formulation |
up to Table of Contents |
next: Flux Schemes > |
| open User's Guide (in
this window) open Applet Page (in new window) |
||
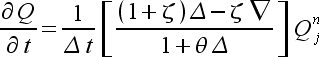
|
(13) |

|
(14) |
|
|
(15) |
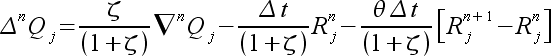
|
(16) |
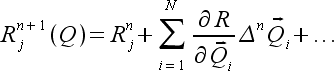
|
(17) |
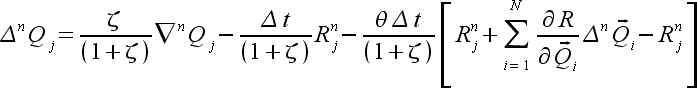
|
(18) |

|
(19) |
| Table 1. Two Parameter Time
Integration Schemes as Programmed in Gryphon |
|||
| theta |
zeta |
local time accuracy |
|
| Euler Implicit |
1 |
0 |
dt squared |
| Euler Explicit |
0 |
0 |
dt squared |
| Leap - frog |
0 |
- 1/2 |
dt cubed |
| Trapezoidal |
1/2 |
0 |
dt cubed |
| 3-point backwards |
1 |
1/2 |
dt cubed |
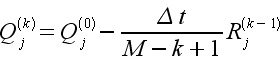 FOR k = 1 to M
FOR k = 1 to M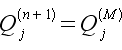
|
(20) |
| <previous: Finite Volume Formulation |
up to Table of Contents |
next: Flux Schemes
> |