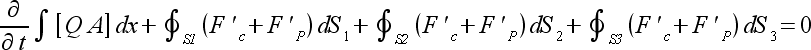
| <previous: Variable Definitions |
up to Table of Contents |
next: Time Integration
Schemes > |
| open User's Guide (in
this window) open Applet Page (in new window) |
||
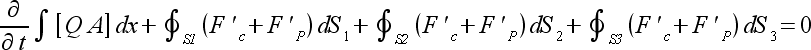
|
(6) |

|
(7) |
| |
(8) |
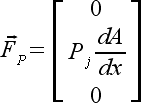
|
(9) |
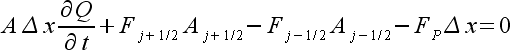
|
(10) |

|
(11) |
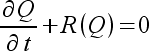
|
(12) |
| <previous: Variable Definitions |
up to Table of Contents |
next: Time Integration
Schemes > |