| <previous: MUSCL
Differencing |
up to Table of Contents |
next: References > |
| open User's Guide (in
this window) open Applet Page (in new window) |
||
| |
(75) |
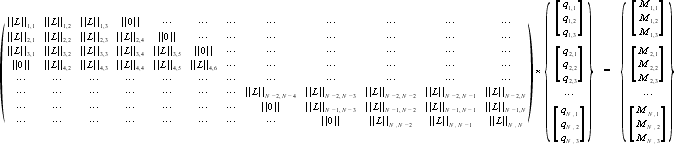
(click image to enlarge scale - opens in a new window) |
(76) |
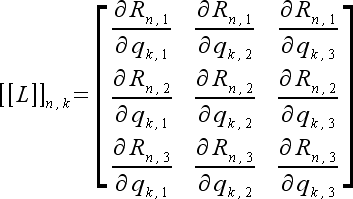
|
(77) |
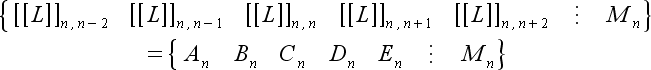
|
(78) |
| |
(79) |
| |
(80) |
| |
(81) |
| |
(82) |
| |
(83) |
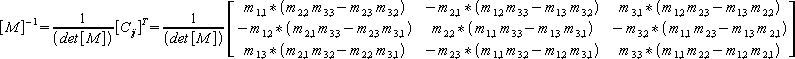
(click image to enlarge scale - opens in a new window) |
(84) |
| <previous: MUSCL Differencing |
up to Table of Contents |
next: References > |