| <previous: Van Leer Flux
Splitting |
up to Main Flux Page |
next: AUSM Flux Splitting
> |
| open User's Guide (in
this window) open Applet Page (in new window) |
||
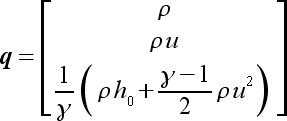
|
(33) |
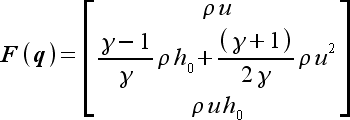
|
(34) |
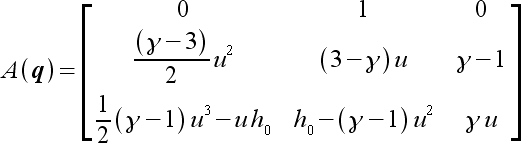
|
(35) |
| (36) |
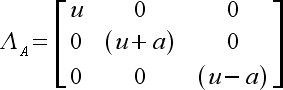
|
(37) |
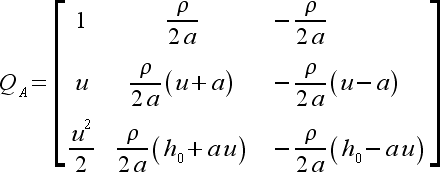
|
(38) |
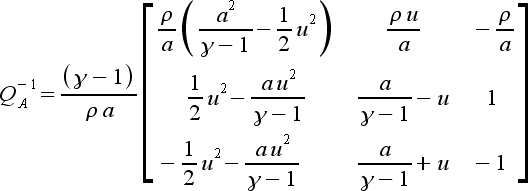
|
(39) |
| (40) |
| |
(41) |
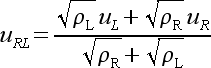
|
(42) |
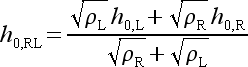
|
(43) |
| (44) |
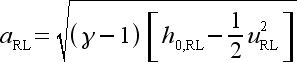
|
(45) |
| (46) |
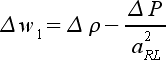
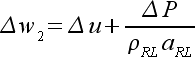
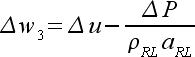
|
(47) |
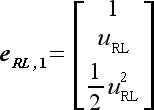
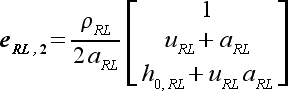
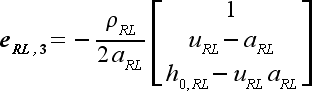
|
(48) |
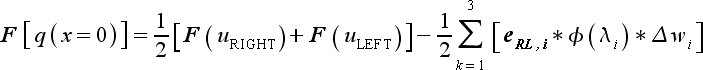
|
(49) |
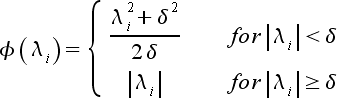
|
(50) |
| (51) |
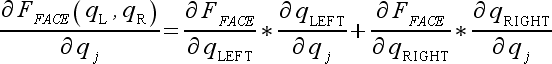
|
(52) |
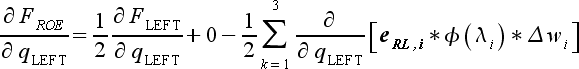
|
(53) |
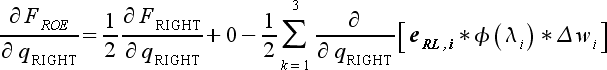
|
(54) |
| <previous: Van Leer Flux
Splitting |
up to Main Flux Page |
next: AUSM Flux Splitting
> |