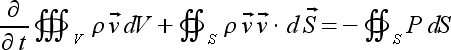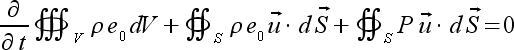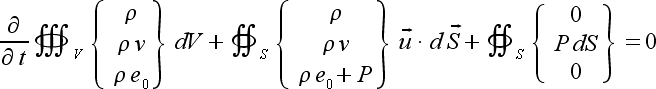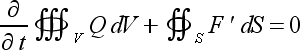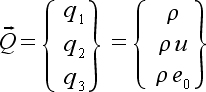The Governing Equations for Inviscid,
Compressible Quasi 1D Flow
Quasi 1D flow represents a situation in which the
fluid is restricted to motion along one coordinate in space, but for which
the effective cross-sectional area of the fluid domain is allowed to vary
along that coordinate direction. The governing equations for this
fluid motion are derived beginning from the integral form of the Navier-Stokes
equations. The flow is considered to be inviscid and without body
forces, and the formulation requires a total of three equations: continuity,
x-direction momentum, and energy. A typical fluid element is pictured
in Figure 1.
Figure 1. A Typical
Quasi-1D Fluid Element
For this situation, the integral form of the governing
equations are given as follows:
These equations are presented here without derivation.
The derivations from basic principles can be found in Anderson[].
Note that this formulation can be written in vector form by combining
the three above relations into one.
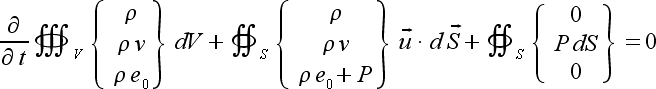
|
(4)
|
The three equation set can be written in a single form for brevity.
The application of the finite volume formulation applies to each equation.
The prime appears in the flux term because the sign of the flux must
be accounted for in taking the integral (as the dot product has been removed
from the previous equation).
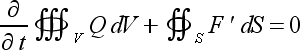
|
(5)
|
This form is called a "conservative" form. Using the conservative
form of the Euler equations is desirable because discontinuities like shocks
are admitted automatically as part of the solution with no special action
necessary. The variables making up the vector Q are called the conservative
variables. All solution is done in terms of these three conservative
variables, so primitive variables which might be of more interest (things
like velocity, pressure, etc.) must be calculated as functions of the conservative
variables. Fortunately, the three conservative variables completely
define the one dimensional flow field, and any other flow variable can be
calculated form them as shown in the next section.
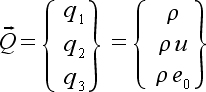
|
(6)
|